. : RSA Encryption : .

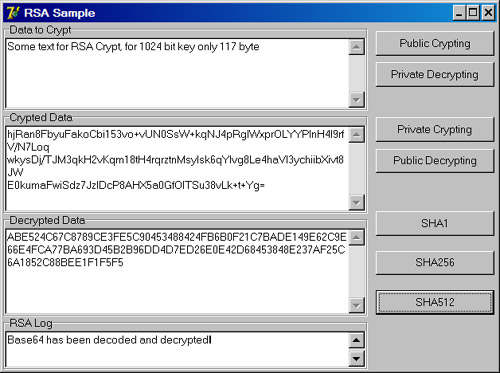
Исходник программы, показывающей пример исследования алгоритма обмена открытым ключом RSA. Это усовершенствованная система шифрования RSA.

Принцип шифрования

Имеются открытый и закрытый ключи, каждый из которых состоит из двух значений. Для открытого ключа значениями являются n, «модуль», и e, «магическое» целое число для шифрования. Значения закрытого ключа - это n, то же значение модуля, которое появляется в открытом ключе, и d, число, которое может расшифровать любой текст, зашифрованный с использованием открытого ключа.

Программа содержит простой рабочий пример с использованием маленьких ключей и имеет страницы, позволяющие «Алисе» и «Бобу» имитировать обмен зашифрованными сообщениями. Поддерживаются значения ключевого модуля длиной от 16 до 1024 бит. Кстати, удобное практическое правило для преобразования между размерами двоичных и десятичных чисел состоит в том, чтобы умножить двоичную длину на 0,3, чтобы получить десятичную длину. Таким образом, программа обрабатывает ключи длиной примерно от 6 до 300 цифр. Длина ключевых модулей имеет два значения:

• Метод генерации RSA зависит от того, что, как правило, сложно разложить на множители число, которое является произведением двух «больших» простых чисел. Таким образом RSA определяет значение n. Если известны два простых множителя n и публичное значение e, частное значение d можно было бы вычислить, а это плохо!
• Значение n также определяет количество различных значений обычного текста, которые могут быть зашифрованы. Таким образом, с большим n мы можем объединить несколько символов в один блок, и вместо 26, 128 или даже 256 возможных чисел, которыми могли бы играть плохие парни, мы можем расшифровать миллионы или триллионы многосимвольных фраз. орешек сложнее расколоть.

Для небольшого математического примера мы можем вычислить размер блока для модуля ключа из 300 цифр, если мы хотим иметь возможность зашифровать все 256 возможных значений однобайтовых символов. Требуется, чтобы 256x <= 10300, или, принимая логарифм с обеих сторон, x log (256) = 300 log (10), поэтому, поскольку log (10) = 1, x = 300 / log (256) = 300 / 2,41 = 124,5 или 124 символа в блоке.

Использование программы должно быть очевидным. Есть пара страниц текста, описывающего вычисление ключей после выбора трех независимых переменных (два простых числа и значение e) и теории, лежащей в основе «подписи» сообщения, что доказывает, что отправитель является тем, кем они себя называют. На последних двух страницах представлены традиционные корреспонденты, Алиса и Боб, которые могут обмениваться сообщениями, надеюсь, с минимальным обучением с нашей стороны, чтобы помочь им.

Примечания

Математика, лежащая в основе генерации ключей RSA, хорошо известна. Фактически, публичное раскрытие алгоритма шифрования / дешифрования является одним из основных принципов программных криптографических систем. Методы BigInt GCD, InvMod и ModPow существовали в прошлых версиях и используются для генерации ключей и шифрования / дешифрования сообщений в этой программе. Программа тестирования BigInts позволяет тестировать эти функции со значениями, вводимыми пользователем, и была удобным инструментом для ручного выполнения необходимых операций во время разработки кода.

Самая сложная часть кода была в процедуре MakeRSAKey, в частности, обрабатывающей блокировку. Мне потребовалось больше времени, чем следовало бы, чтобы осознать, что, хотя операции шифрования / дешифрования являются симметричными (т.е. шифрование с использованием закрытого ключа и шифрование с помощью открытого ключа работают так же хорошо, как и наоборот), отдельные процедуры шифрования и дешифрования являются обязательными. Хотя мы можем брать символы размера блока во время шифрования, зашифрованный текст состоит из чисел, которые дополняются (с нулями слева) до количества цифр в модуле ключа. Следовательно, при расшифровке мы должны брать символы модульной длины за раз, а не символы размера блока.