Исходник программы, показывающей пример анимированной симуляции трех разновидностей маятника: простого, двойного и принудительного.
Программа исследует три различных типа маятников. Каждая из вкладок позволяет пользователю установить параметры, определяющие маятники, и привести их в движение для наблюдения за эффектом. Программа была написана для проверки недавно разработанного метода Рунге-Кутта для решения одного обыкновенного дифференциального уравнения (ОДУ) или системы ОДУ.
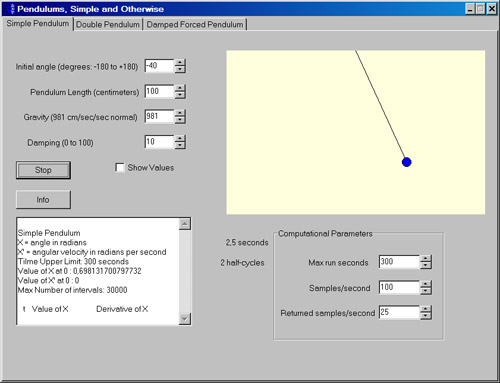
Простой маятник
Простой маятник состоит из груза или «боба», свободно свисающего с конца невесомого стержня длиной L. Вращение боба на некоторый начальный угол q0 и его отпускание сообщает его движение. Гравитация, G, тянет боб по дуге вниз и за вертикаль до угла, равного начальному смещению, если некая демпфирующая сила не замедляет его. Коэффициент демпфирования D - это постоянная величина, которая при умножении на угловую скорость q дает силу, уменьшающую скорость.
Другими словами, ускорение боба равно той части силы тяжести, которая действует перпендикулярно валу, за вычетом демпфирующей силы. Знак минус в термине гравитации просто говорит нам, что гравитация здесь враг, всегда пытаясь замедлить процесс.
Наша процедура Рунге-Кутта вызывает определяемую пользователем функцию, передавая угол (q) и угловую скорость (q ') для каждого временного интервала. В этом случае функция применяет указанное выше уравнение для возврата нового значения углового ускорения (q '').
В примере можно менять силу тяжести, длину, начальный угол и коэффициент демпфирования и наблюдать за движением маятника.
Кстати, часто предполагается, что период маятника (время полного поворота) не зависит от длины, массы или угла поворота. Это почти правда. Маятник качается быстрее при меньших углах, в чем вы можете убедиться сами, установив коэффициент демпфирования на 0 и рассчитав 10 колебаний для различных начальных углов.
Примечание: все углы измеряются против часовой стрелки с юга (вниз).
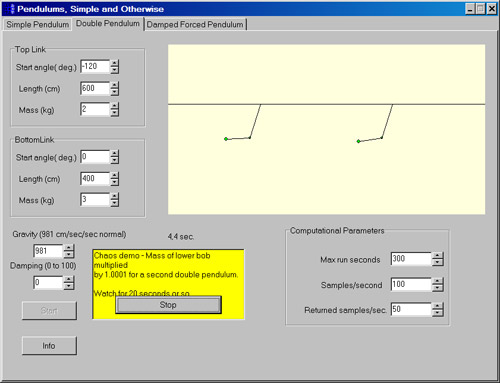
Двойные маятники
На второй вкладке один маятник прикреплен к концу другого маятника, как если бы вы держали гирю в руке и раскачивали ее плечом и локтем. В отличие от простого маятника, уравнения для двойного маятника учитывают еще и массы качелей.
Здесь мы проверяем способность нашей процедуры Рунге-Кутта решать систему дифференциальных уравнений. Для каждой части маятника существуют отдельные ОДУ, и они взаимодействуют, то есть на ускорение каждого боба влияет ускорение другого.
Данная вкладка включает демонстрацию эффекта «хаоса»; небольшое изменение, приводящее к совсем противоположному поведению. В этом примере с «двойным двойным маятником» мы клонируем заданный маятник, умножаем массу нижнего боба на 1.0001 на клоне, а затем одновременно отпускаем их. Через минуту или две поведение изменится и не будет иметь очевидного отношения друг к другу. Поиск в Интернете по запросу «эффект бабочки» даст интересные сведения об этой чувствительности к начальным условиям.
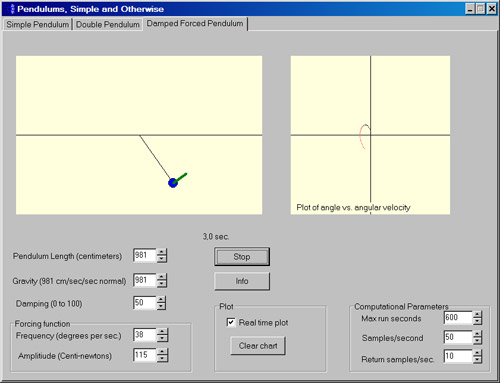
Принудительный маятник
На последней вкладке можно поиграть с демпфированным вынужденным маятником. В этом случае к простому маятнику прикладывается сила заданной амплитуды A и частоты ? (омега). Уравнение часто упрощается, предполагая, что длина маятника равна значению силы тяжести, поскольку интересные эффекты включают коэффициент демпфирования D и характеристики частоты воздействия в момент времени t.
Анимация маятника отображает приложенную силу в виде зеленой полосы, действующей на боб под прямым углом к маятнику и длиной, пропорциональной значению силы.
Также отображается отдельная диаграмма зависимости угла маятника от угловой скорости. Для стабилизации маятника может потребоваться минута или больше из-за демпфирующих эффектов, когда он стартует из положения покоя. Также есть флажок «В реальном времени», который переключает отображение между режимом реального времени и максимальной скоростью отображения для вашего компьютера и видеокарты.
Соответствующий выбор входных значений приведет к созданию шаблонов, которые повторяются в одиночных, двойных циклах или хаотичном поведении, которое может никогда не повториться. Начиная со значений по умолчанию, попробуйте прогоны с амплитудами от 100 до 120, чтобы увидеть различные интересные поведения.