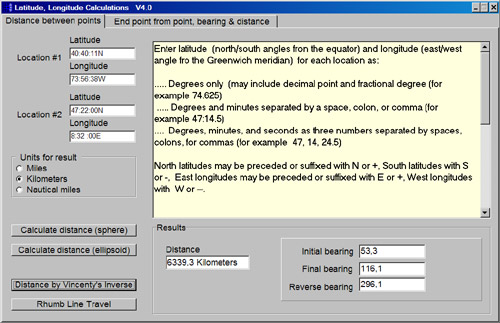
Исходник программы, показывающей пример расчета расстояния на поверхности между двумя точками на Земле, определяемое их широтой и долготой.
Широта и долгота представляют собой угловую часть точки в пространстве, определенную в полярных координатах. Напомним, что в двухмерном пространстве точка может быть определена как декартовыми, так и полярными координатами. Декартова координата определяет местоположение как горизонтальное и вертикальное расстояние от некоторой фиксированной точки, начала координат. Полярные координаты определяют точку по длине и углу отрезка линии от начала координат до точки. Теперь, если мы представим точку на плоской двухмерной странице, определяемую двумя числами, а затем мы хотим переместить точку в трехмерное пространство, поднявшись со страницы, нам понадобится еще одно число. Для декартовых координат третьим числом будет высота точки над страницей. Для полярных координат мы повернем сегмент линии вверх за пределы страницы и измеряем вертикальный угол от страницы до линии.
Широта и долгота - два полярных координатных угла. Если мы представим себя в центре Земли, а макушка головы будет направлена ??к Северному полюсу, а ногами - к Южному полюсу, то экватор будет расположен под углом 90 градусов к северу - прямо перед нами. Эта воображаемая линия вокруг Земли под углом 90 градусов к северному полюсу определяется как точка отсчета 0 для измерения широты, угловой координаты точки север-юг. Другая воображаемая линия, идущая на север и юг вдоль поверхности земли и проходящая через полюса и Гринвич, Англия, является точкой отсчета 0 градусов для измерения углов восток-запад, долготы. Широта находится в диапазоне от 90 градусов северной широты до 90 градусов южной широты, при этом южные углы считаются отрицательными. Долгота колеблется от 0 до 180 градусов к востоку и западу с отрицательными углами на запад.
Фактическая математика для вычисления расстояния между двумя точками проста и выводится во многих местах сети, а именно: угловое расстояние = arccos (Sin (lat1) * Sin (lat2) + Cos (lat1) * Cos (lat2) * Cos ( lon1-lon2)) и предполагая, что угол задается в градусах, расстояние = расстояние на градус * угловое расстояние = (2 * Pi * радиус / 360) * угловое расстояние. Это оценка сферического расстояния, полученная с помощью этой программы.
Вышеупомянутое объяснение говорит нам о том, что третий параметр полярной координаты, определяющий точку, длину отрезка линии, является постоянным (радиус Земли). Но на самом деле Земля не сферическая. Наше вращение привело к тому, что Земля слегка вздулась на экваторе и упала на полюсах. Сэр Исаак Ньютон в 1600-х годах рассчитал, что радиус на полюсах равен 0,9967 радиуса на экваторе. Текущее значение составляет около 0,9966, так что сэр Исаак поступил неплохо. Разница между двумя окружностями (полярной и экваториальной) составляет около 83 миль, поэтому сферические координаты для двух точек на экваторе, но разнесенных на 180 градусов, должны давать максимальную ошибку, около 40 миль. Между прочим, эти оценки расстояния являются «оценками большого круга», что означает, что они лежат на пути, определяемом плоскостью через две точки плюс центр Земли и поверхность Земли. Маршрут большого круга - это кратчайшее расстояние между двумя точками. Как ни странно, если вы находитесь к северу от экватора и хотите добраться до точки прямо к востоку от вашего текущего местоположения, не направляйтесь на восток - самый короткий путь - начать путешествие на северо-восток и прибыть на юго-восток!
Расчет расстояний с учетом эллиптической формы Земли довольно сложен. Однако вычисления, которые, наиболее близки к истинному расстоянию, используют сферический макет Земли.