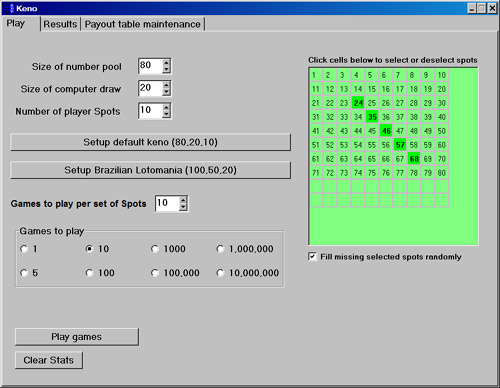
Исходник программы, показывающей пример имитации игры Кено в казино.
Кено - древняя азартная игра, которая каким-то образом проникла в казино. Насколько нам известно, никакие навыки или стратегия не могут снизить ваши шансы на проигрыш в долгосрочной перспективе. Все игры, предлагаемые казино, рассчитывают на то, что вы «в конце концов» проиграете.
Чтобы сыграть в Кено, заплатите немного денег за каждую игру, обычно 1 доллар, а затем выберите от 1 до 10 чисел (15 в некоторых версиях) от 1 до 80. Затем оператор игры выбирает 20 чисел из 80. Вам платят на основе от двух факторов: количества выбранных вами чисел и числа, совпадающего с 20 выпавшими числами. В таблице выплат указано, сколько вам будет возвращено за каждый результат.
Кено имеет небольшой собственный словарный запас:
- Споты - это числа, выбранные для игры.
- Пул - это набор чисел, из которых выбираются точки. Целые числа от 1 до 80 во всех случаях, которые я видел.
- Жеребьевка - это числа, нарисованные для сопоставления с точками.
- Захваты - это точки, которые совпадают с числами в розыгрыше.
- Таблица выплат или ставок указывает, сколько денег вы получите за каждый выигрыш. Если его нет в таблице, ваша выплата равна нулю.
- «Процент заведения» определяет, какая часть полученных денег возвращается в качестве выигрыша. Это может составлять от 5% до 30%.
Программа позволяет играть от 1 до 10 спотовых игр. Вы можете выбрать ставки самостоятельно или позволить программе выбирать числа случайным образом. Кнопки позволяют играть в одну игру, в раунде из 5 игр, в котором одни и те же места сохраняются от игры к игре, в 20 раундах по 5 игр для моделирования 100 игр за раз или в 100 000 игр для проверки статистических результатов. Для всех, кроме кнопки «100 000 игр», перечислены результаты каждой отдельной игры, включая выплату и общую выплату для всех игр с момента последней очистки статистики.
Таблица начальных выплат - это «справедливая» таблица с выплатами, основанными на вероятности каждого исхода и отсутствием прибыли для заведения.
Немного математики
Самой интересной частью проекта было определение вероятностей для каждого возможного результата. Вероятность любого события определяется как количество успешных исходов события, деленное на общее количество возможных исходов. Допустим, мы играем в игру с 5 точками и хотим рассчитать вероятность того, что произойдет 3 улова. Общее количество успешных результатов - это количество способов, которыми мы можем выбрать наши 3 улова из 20 выпавших номеров, умноженное на количество способов, которыми 2 несовпадающих числа могли быть вытянуты из других 60 номеров, не участвующих в розыгрыше. Эти числа выдает функция «комбинации». Если мы используем общую терминологию C (N, R) для обозначения выбора R из N элементов, то C (20,3) x C (60,2) представляет количество возможных результатов. Общее количество исходов C (80,5), а вероятность будет C (20,3) x C (60,2) / C (80,5).
Поскольку порядок не имеет значения по определению, C (20,3) является произведением 20 вариантов выбора для первого числа, 19 вариантов для второго и 18 вариантов для третьего, разделенных на количество порядков трех чисел ( обозначается как 3 факториал = 3! = 3x2x1 = 6). Итак, C (20,3) = 20x19x18 / 6 = 1140. Точно так же C (60,2) = 60x59 / 2 = 1770, и общий возможный успешный результат = 1140 x 1770 = 2,017,800. Делитель C (5,80) вычисляется компьютером и равен 24 040 016. Итак, C (20,3) x C (60,2) / C (80,5) = 2017800/24040016 = 0,08393505 или около 8 игр из каждой сотни сыгранных. Ух! Сделайте это еще 65 раз, и у нас будут вероятности для всех исходов от 0 до N уловов для всех N от 1 до 10.