Исходник программы, показывающей пример создания и исследования алгоритма, соединяющего все точки на плоскости и объединенного общим интерфейсом.
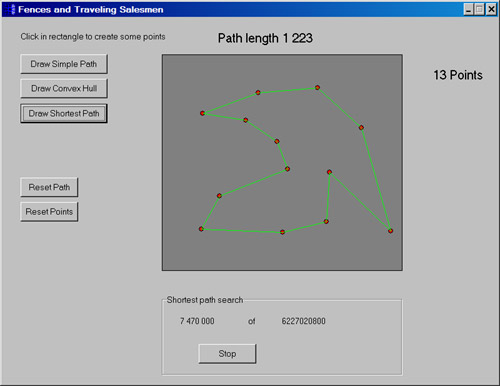
Показаны три алгоритма «соединения всех точек» на плоскости, объединенных в программе общим интерфейсом.
- «Simple Path» соединяет произвольное расположение точек без пересечения линий.
- Алгоритм «Convex Hull» может очертить «забор» минимальной длины вокруг любого набора точек со свойством, что все внутренние углы меньше 180 градусов. Если бы точки были колышками, то кусок веревки, обернутый вокруг колышков, определил бы выпуклое место.
- Наконец, «Shortest Path» решает проблему коммивояжера. Например, продавцу товаров необходимо посетить несколько городов и спланировать свой маршрут так, чтобы пройденное расстояние было как можно короче.
«Simple Path»
Сам метод решения этой проблемы довольно прост. Мы начинаем с точки с одной из крайних координат, скажем, с максимальным значением Y. Затем рассмотрим линии, образованные путем соединения этой точки с любой другой точкой на набор. Вычислите угол от горизонтали для этих линий и отсортируйте по этому углу. Путь от начальной точки к каждой из отсортированных точек последовательно и обратно к начальной точке представит собой простой замкнутый путь.
«Convex Hull»
Выберите точку (наибольшее значение Y) и рассчитайте угол от этой точки до любой другой точки - выберите точку с наибольшим углом (или минимальным углом от горизонтали) и проведите линию к этой точке. Идея состоит в том, что мы совершим один полный оборот, когда добавим все точки корпуса. Повторите действие, начиная с только что добавленной точки с ограничением, что новая точка - это точка с наименьшим углом, который в тоже время больше, чем предыдущий угол. Продолжайте, пока не вернетесь к начальной точке.
Вы можете попробовать это сами, например так:
- Нарисуйте на листе бумаги несколько точек и выберите самую низкую, P1.
- Нарисуйте линию, идущую горизонтально вправо, и поместите карандаш на эту линию так, чтобы конец ластика карандаша был на P1.
- Удерживая конец ластика на P1 (или Pn), вращайте карандаш против часовой стрелки, пока не коснетесь точки P2 (Pn + 1), которая будет следующей точкой на корпусе.
- Проведите линию от P1 до P2 (от Pn до Pn + 1) и проведите карандашом по этой линии, пока ластик не окажется на P2 (Pn + 1).
- Повторяйте шаги 3 и 4, пока не вернетесь к P1 и корпус не будет готов.
Шаг «скольжения карандаша» заставляет нас вращаться вокруг корпуса. Эквивалент программы - сохранение каждого угла в переменной prevangle и игнорирование всех углов, меньших, чем prevangle, при поиске. Наименьший угол больший, чем предыдущий, будет выбран в качестве следующей точки.
«Shortest Path»
Одна из большого класса задач называется NP-полной (недетерминированной полиномиальной полнотой). Этот термин относится к классу задач, для которых не известно решение за полиномиальное время, но не было доказано, что такого решения не существует. Задачи, которые могут быть решены за полиномиальное время, имеют время решения, пропорциональное некоторой комбинации степеней количества элементов. Проблемы, которые не являются полиномиальными, являются экспоненциальными и время их решения увеличивается пропорционально некоторой функции, включающей количество элементов в качестве степени (например, 2N). Исчерпывающий поиск, требующий N факториальных (N!) операций, является одним из «или худших» случаев.
Представленная здесь версия использует «грубую силу» - технику исчерпывающего поиска, проверяя длину пути для каждого возможного порядка посещения городов. Она может проверять от 50 000 до 200 000 путей в секунду и работает нормально до 10 точек (проверено 3,6 миллиона путей). Это никогда не решит дело 15 городов (около триллиона, 1012 путей). Предварительно отсортировав точки так, чтобы каждая из них находилась рядом со своим ближайшим соседом, мы всегда сможем найти пути, которые выглядят довольно логичными за разумный период времени.