|
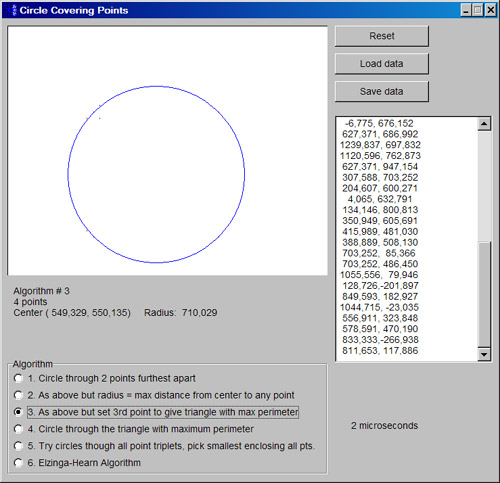
Исходник программы, показывающей пример как нарисовать на листе бумаги несколько точек и обвести их как можно меньшей окружностью.
Наиболее цитируемый алгоритм решения данной проблемы был предложен профессорами Эльзингой и Хирном, которые в 1972 году опубликовали геометрический алгоритм решения этой проблемы и доказали его правильность.
Алгоритм
- Выберите любые две точки: Pi и Pj.
- Постройте круг, центр которого находится в середине линии, соединяющей Pi и Pj, и которая проходит через Pi и Pj. Если этот круг содержит все точки, то центр круга является оптимальным X. В противном случае выберите точку Pk вне круга.
- Если треугольник, определяемый параметрами Pi, Pj и Pk, является прямоугольным или тупым, переименуйте две точки напротив прямого или тупого угла в Pi и Pj и переходите к шагу 2. В противном случае эти три точки определяют острый треугольник. Постройте круг, проходящий через три точки (центр - это пересечение серединных перпендикуляров двух сторон треугольника). Если круг содержит все точки, остановитесь, иначе перейдите к шагу 4.
- Выберите точку Pl, не входящую в круг, и пусть Q будет точкой среди {Pi, Pj, Pk}, которая находится на наибольшем расстоянии от Pl. Увеличьте диаметр (от центра круга) через точку Q до линии, разделяющей плоскость на две полуплоскости. Пусть точка R будет точкой среди {Pi, Pj, Pk}, которая находится в полуплоскости напротив Pl. С точками Q, R и Pl перейдите к шагу 3.
Эта процедура казалась намного более сложной, чем необходимо, поэтому я наивно попробовал несколько других техник, ни один из которых не сработал. Я оставил их все в программе и задокументировал их там, чтобы проиллюстрировать процесс решения проблемы. На самом деле мой 5-й метод, кажется, работает (думаю, я заново открыл классическое решение), просто он намного медленнее, чем у Эльзинга-Хирн. Мой № 5 предполагает, что наименьший круг, содержащий все точки, пройдет через 3 точки. Поэтому мы просто пробуем все возможные трехточечные подмножества нашего полного набора точек, находим круг, определяемый каждым триплетом, проверяем, охватывает ли он все точки, и, если да, сохраняем тот с наименьшим радиусом. Нам также (как и Эльзинга-Хирн) необходимо поймать исключительный случай, когда диаметральный круг, определенный через две наиболее удаленные друг от друга точки, охватывает все точки. Например, учитывая набор из трех почти коллинеарных точек, окружность, определяемая этими тремя точками, будет намного больше, чем необходимо.
Программа имеет простой интерфейс - просто щелкните несколько случайных точек в области изображения и просмотрите результаты. Радиокнопки позволяют выбрать алгоритм для использования. Просмотры: 1 491
Скачивания: 15
|

